連作空間と楽しい線形代数学のはなし
表題の通り東北大短歌3号の浅野さんの「連作空間論」を読んだはなしと、楽しい線形代数のはなしをします。
「連作空間論」は、短歌連作というもの自体について理論を立てたり議論したりすることが必要だ、という問題意識から、線形空間という数学の概念を借りてきて連作について理論を立ててみた、という評論だと思っています。連作を線形空間の比喩で構造化することについて、私は納得するところもあったしひっかかるところもありました。
数学ではものの集まりをたんに「集合」と言って、そこに構造が入ったものを「空間」と言うので、「連作空間」というのを妄想するのは非常に楽しい。連作、というのはたしかにうたの集まりだけれど、そこに構造が入っているな。
— Sho YAMASHITA (@Yamashio_) 2016年11月15日
例えば山下さんが上のようなツイートをされていますが、踏まえられている数学の話を知っていると、「連作空間論」にはああ~この話ね、みたいなところがあります。何かを批評するときに、哲学の話を引っ張ったり、フロイトやラカンの精神分析学の話を取ってきたり、ということはまあまああると思います。哲学も数学も、人間が考えうるすべての思考のやり方とか枠組みの総当たり戦みたいな要素があると私は思っている(精神分析学については正直良くわからないので困っている)ので、何かについて考えるとき、数学的な比喩を使ったっておかしくないんだと思います。
「連作空間論」における連作の理論化のどこにどうして納得して、どうして引っかかったかを書きたいし、それを線形代数知ってますという人にしか分かってもらえないのもつまらないので、浅野さんが使っている数学の概念についてしばらく書きます。ただ、私の数学的な知識は、特別数学が出来るわけでもないけれどまあ勉強は楽しんでる理学部二回生程度です。勘違いやよくない定式化、補足などがあれば教えていただければうれしく思います。
*
まず、ベクトルとか次元とか空間*1の話をするために、いくつか例え話をします。知ってるよ、て場合は読み飛ばしてもらっても大丈夫です。卵が3個あれば卵焼きが一回作れるというのが正比例です。図で書けば直線です。これは1次元です。卵1個とホットケーキミックス150gと牛乳100mlがあればホットケーキが一回(話を簡単にするために一回と言うけど3枚くらい焼けるかな)焼けるという話もできます。作るのがホットケーキだけならこれも正比例で、空間の中に図示しても直線です。ホットケーキを何枚焼くにしても、卵:ホットケーキミックス:牛乳の比は変わらない、つまり卵100個とホットケーキミックス1.5kgと牛乳10Lを混ぜたものを想像して(あまり想像しやすくはないけど)もらうと、材料は1種類であり、ホットケーキを何枚でもいいからとりあえず焼こうとして買ってくる材料を図に点で打っていくと、これは卵焼きのときと一緒で1次元です(ホットケーキベクトルそれだけでは何次元の空間の中にあっても直線しか構成することができない)。このような空間の中の点は、ある時と場合における買い物袋に入っているそれぞれの材料の量だと思ってください。

(本に載るようなきれいな図が作れたらいいのですが、そういった専用のソフトなどに通じていないので図がざっくりなのはお許しください。)
そして、牛乳500mlとにんじんすりおろし一本でにんじんのスープができる(二人分くらい、コンソメは台所にあるものとする)とか、卵2個とにんじん1本でにんじんしりしりができる(二人分くらい)、とか卵1個と牛乳100mlでプリンができる(砂糖は常備しているものとする)とかを考えて、にんじんスープやにんじんしりしりやプリンを作る話を図にしようとすると、これらを一緒に作るときの買い物袋の中身に対応する点は空間のいろんなところを動きます。
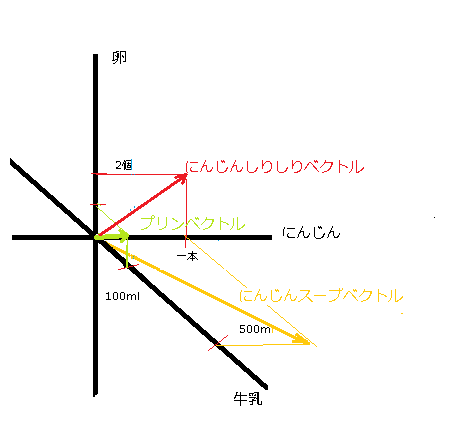
にんじんスープ、にんじんしりしり、プリンを一回つくるのにいい感じの材料をベクトルとして図示してみました。では、にんじんしりしりを一回分、にんじんスープを一人分(一回分の半分)、プリンを3個つくるための材料を考えましょう。これは、(にんじんしりしりベクトル)+ 1/2 ×(にんじんスープベクトル) + 3 ×(プリンベクトル)を足したものです。下の図の青い星ですね。3次元のベクトルを3本足してできるベクトルは、作りたい料理の量のため半分にしたり三倍にしたりした3本のベクトルによって張られる平行六面体の頂点に当たります。

そして実際に買い物袋に何がどれだけ入っているのかは、空間の中の青い星を卵軸やにんじん軸や牛乳軸で読み取るとわかります。

こんな感じですね。線形空間を話すための下準備のつもりだったのですが、食べ物の話をするうちに楽しくなって長くなってしまいました。準備したものをまとめると、
・3次元空間と、その中の3次元ベクトル、そしてそのベクトルによって張られる空間(上の例でにんじん(略)ベクトルたちに好きな数を掛けたりそれらを足したりしてできたベクトルによって与えられる点が移動できる範囲)上の点を例として登場させて、
・1本のベクトルによって張られる空間は1次元、n本の線形独立*2なベクトルによってはられる空間はn次元、
・n次元空間上の点は、最初に設定しておいた直交座標軸によっても表すことができるし、線形独立なn本のベクトルを使ってもそれぞれで一意的に表すことができる、ということです。
*
いったん浅野さんの評論に戻ってみましょう。
ある連作の作品世界を把握するために必要になる評価のための軸を〈連作軸〉と呼び、その個数を〈次元〉と呼ぶ。(…中略)「作品世界という多次元空間」を〈連作空間〉という一語で表すこととする。〈連作空間〉とは、連作という作品が存在している多次元空間であり、そのひろがりは〈次元〉という量によって表現される。 ――浅野大輝「連作空間論」
連作の作品世界が、次元をもった数ベクトル空間*3(中学や高校の数学に出てくる、xyzのような(実)数直線を座標軸にもった空間)ぽい感じで理論化されています。そしてその〈連作空間〉の中に〈基底〉という概念が導入されます。
いま〈連作空間〉を航行する作者の指針を、〈基底〉という語で表そう。そして〈基底〉によって限定される〈連作空間〉中のある範囲を〈基底空間〉と呼ぶことにする。
〈基底〉とはつまり、〈連作空間〉の内部の事物を、その性質や概念などに応じて繋ぎあわせるベクトルである。
基底という言葉が評論にでてくることによって、理論の背景が、数ベクトル空間から線形空間へと、より一般的でいろんな議論ができる場所(数ベクトル空間は線形空間である条件を満たしているものの一つ)になったと思いました。
*
では数学のほうに話を移して線形空間とは何か、という話をします。こんな注釈をいれなくてはいけないことは申し訳ないのですが、あくまで私の理解なので、数学の本を読まれるのがほんとは一番きっちりしていいと思います。
線形空間の数学的な定義はこんなです。
集合Vと体*4K(=ℝ*5またはℂ*6)を考え、Vの2つの元の加法+とVの元にKの元をかけるスカラー倍を定める。このとき、ここで定められた加法とスカラー倍が次の条件を(1)ー(8)を満たすとき、VをK上の線形空間という:a,b,c∈*7Vとしα,β∈Kとする。
(1) a + b = b + a
(2) a +(b + c) = (a + b) + c
(3) Vには零元0*8が存在し、すべてのa∈Vに対して、a + 0 = a を満たす。
(4) 各a∈Vには逆元と呼ばれるb∈Vが存在し、a + b = 0 を満たす。
(5) 1a = a
(6) α(a + b) = αa + αb
(7) (a + b)α = αa + αb
(8) α(βa) = αβa
集合Vの中の要素に足し算が定義されているし私たちが普通の数だと思うものとの掛け算も定義されているし(そしてその加法乗法の結果変なものがでてくるのではなくちゃんとVの要素がでてくるし)、順番を変えたりしても大丈夫って感じの話だと思っています。私の理解では、線形空間とは1次元でも2次元でも3次元以上でも、直線や平面や空間(空間って言葉あんまり使うのどうかと思いますがこの3次元の世界を指して代用できる単語が見つからない)の話をするn次元座標空間をめちゃ一般化したものです。そう、変な感じはしますけど、座標の原点を通る直線(上の点の集合)も1次元の線形空間です。他にも、m×n次行列の集合とか、実数の区間I上の実数値連続関数の全体(つまり区間Iの実数を実数全体へ写す写像の集合)とかも線形空間の条件を満たして線形空間です。m×n次行列の線形空間の次元はm×nですが、関数空間は無限次元です。線形空間はベクトル空間とも呼ばれますし、どっちもけっこうメジャーな呼び方な気がします。今までベクトルという言葉を特にことわりなく使ってましたけど、線形空間(ベクトル空間)の元をベクトルと言います*9。
そして、線形空間というものを取り扱うときに欠かせない概念が次元と基底です。
……
お疲れ様です、私も疲れました。
今後にむけたメモ、もしくはダイイングメッセージ
- 数学からの次元と基底のはなし
- 短歌というベクトルの集合である連作によって張られる線形空間が連作空間ということでいいだろうか:span ( 短歌, 短歌, 短歌,,,,, ) = 〈連作空間〉
- 短歌に交換可能な加減乗法は成立するか、短歌ではなく、〈短歌を読んだ時の感じ〉を集合の元としてみると…?(これ自体は言いがかり的というか、必ずしも線形空間のモデルに一致する必要性はないだろうけど)
- 私の思ってる線形空間における基底と評論の〈基底〉が一致しなくて評論の〈基底〉理解に不安がある
- 基底空間が分からない(評論内部での位置づけと背景にあるならば数学の用語と両方)
- 〈連作軸〉と線形空間の基底は一致しないのか(私のイメージでは基底をとってそこから評価を考えてもよさそうな気がしてしまうしそのへん同一視してしまう、そうすると基底は自由にとれるから、批評のときによくある同じことをみんな違う言い方するという現象にも対応する気がする。ちなみに数学における軸ってどういう概念だっけ?直交してないとだめ?)
- 無限次元線形空間(関数空間)へのロマン:〈連作空間〉は無限次元線形空間なのではないか。しかし私は無限次元線形空間の存在しかしらないので、雰囲気しか知らない難しくてすごそうなものに勝手にロマンティシズムを押し付けているだけかもしれない(たぶん私が知ってるものに対してそういうことされたら普通に腹が立つと思う)。
- 〈基底変換〉と批評をやりとりすること
- 連作を読む/批評する過程とは与えられた短歌というベクトルから読み手が〈連作空間〉を構成し、〈基底〉or〈正規直交基底〉を定めることである。次元が多ければいい作品とかではなく、〈連作空間〉を我々に構成させる力がどのくらい強く働いているか、みたいな〈連作空間〉や〈基底〉に我々がたどりつく過程それ自体が連作の批評である。というふうなのだとその構造的同型性はすごい共感する。あと、一番よく見えるように連作を読もうとする批評は〈連作空間〉の記述になるのではないか。ただ、連作の次元が明示的に数として表されたり、連作がベクトル関数や滑らかな曲線として意識しようというのはなぜか(なぜだろう)納得できない。
- 作品それだけでは、それがどのような連作か、という批評は存在しないので、線形空間の中にプロットできるものの対応物として連作があります、というのは神の視点の議論ぽくて違和感もある。もちろん読みの話も後半でされているしモデル化とはそういうものなのかもしれないけど。
- モデル化という批評:それがたとえいろんなものを取りこぼしてしまうとしても語らないという選択肢はないし、取りこぼしたものは拾いにかえりたい。
*1:山下さんが言った集合に構造を導入してそう呼ぶ空間というより、直線―平面―空間という話をするときの空間のほうをイメージしてほしくて空間って言ったんですけど、空間という語彙の適切な使い方について正直良くわかってません。座標によって指定された点の集合があり、その点の集合に構造が入っている、と思えばn次元空間(n=1~∞)は構造を持った点の集合としての空間であり、とくにn=3の場合は何次元か述べずに空間と言うって感じなのかしら……
*2:それぞれ違った向きをむいているベクトルたちの集まりを指して線形独立なベクトルと思えばいいと思います。違った向きというのはざっくりすぎる言い方で、線形独立なベクトルの組の中のどのベクトルも、ほかのベクトルを拡大縮小したり足しあわせても表すことができないという状態です。あとで数学の定義も書きます。さっきの例をまた使うなら、(もう家にあったホットケーキミックスをあてにして)卵2個とにんじん1/2本と牛乳100mlを買い物するにんじんケーキベクトルを考えた場合、にんじんケーキベクトルとにんじんしりしりベクトルとプリンベクトルは線形独立ではありません。なぜならその買い物はプリン1個(卵1、牛乳100)とにんじんしりしりを1/2回分(卵1、にんじん1/2)作ろうと買い物をするときと同じ(にんじんケーキベクトルはにんじんしりしりベクトルとプリンベクトルによって張られる平面の上にある)だからです。
(にんじんケーキベクトル)=1/2×(にんじんしりしりベクトル)+(プリンベクトル)
線形独立でないベクトルの組を線形従属といいます。にんじんしりしりベクトルとプリンベクトルとにんじんケーキベクトルが線形従属なら、にんじんしりしりベクトルとプリンベクトルとにんじんケーキベクトルとにんじんスープベクトルも線形従属です。
*3:この辺わからなくて困っているんですけど、ユークリッド空間と数ベクトル空間(たとえば(2,1,0)とかのn個の数の組の集合)は(同型だろうけど)まったくおなじ概念ではなく、数ベクトル空間と座標空間は同じ概念と見做してよいのですかね?? とりあえず見做させてください
*4:体:普通の(順番を変えたり複数回おこなっても答えが変わらない)足し算と掛け算ができて、その答えも自らのうちに含む数の集合のこと。当座の理解では私たちが知ってる数だと思って大丈夫です。つまり掛け算足し算はあたりまえでなくて、それが普通じゃないものについても想定しているわけですよね。数学のこういうところさいこーじゃないですか?そうやっていろんなことが自明じゃないかもしれないってやるから定義の文章とかがややこしくなるんですが……
*5:ℝ:実数real numberの記号
*7:∈:含まれる、という記号。ここではa,b,cがVという集合の要素であることを示す
*8:数学の記号に太字が出てきたら、ベクトルを表している。これは数字のゼロではなくて、ゼロベクトルの意味
*9:正直ベクトルって最初は大きさと向きを持った有向線分だって習った気がしますし、行列とか関数とか普通ベクトルと思わないものもベクトルになってしまうので私はちょっと混乱しています。でも、こういう名前の付け方は「幸福な同一視」と先生は言っていて、たしかに同じように扱って議論できるようになるということでは便利なんですかね。