連作空間と楽しい線形代数学のはなし―その２

　東北大短歌３号浅野大輝「連作空間論」を読んで考えたことを書く、続きです。

gohannmogumogu.hatenablog.com

話を再開する前に、どういう立場でこれを書いているのか補足しておきます。

・〈連作空間〉は比喩：

ここで区別したいのは、物事を数学的な概念を利用して説明してみよう、という論と、実際に物事に数学的な構造があって概念が拡張されるよ！*1という論です。「連作空間論」は前者なので、浅野さんが後半に議論を拡張していく、連作を式で書いてみたりベクトル解析することは今のところ有意味ではないと思っています。だって本当の意味で線形空間ではない*2ため、自然な定義の延長ということがそもそもできません。比喩としてありかどうかは分かりません。対応関係を新たに定義して、納得できる例をだしてもらったら納得すると思います。

・楽しい線形代数学：

私は、この記事が連作の読みや構造の理解に役に立つと思って書いていない節があります。「連作空間論」は線形代数の話を背景にしつつ、ちゃんと連作をどう議論するかという話をしていますが、私は線形代数自体とか、概念をぐりぐりするのが楽しいという話をしています。数学を分かんない、ひい～って言いながら勉強するのは楽しいです。私は自律心がないので、大学の授業がなければ自分でできたかあやしいですが。

　今回の記事では、浅野さんが導入した概念の線形代数的定義を確認します。前記事に引用したように、導入されている概念は〈連作軸〉、〈次元〉、〈連作空間〉、〈基底〉、〈基底空間〉でした。私の対応予想はこれです。

連作空間論―線形代数学

〈連作空間〉―線形空間

〈次元〉ー（線形空間の）次元

〈基底〉ー（線形空間）基底（？）

〈連作軸〉―（扱っている線形空間が有限次元数ベクトル空間／有限次元座標空間であると考えて？その）座標軸（？）

〈基底空間〉ー？？？

 線形空間

　前回は、平面座標、空間座標空間とかベクトル空間をめちゃめちゃ一般化したものとして線形空間というものがあります、という話をしました。定義は大事なのでもう一回載せますね。

 集合Vと体*3K（＝ℝ*4またはℂ*5）を考え、Vの２つの元の加法+とVの元にKの元をかけるスカラー倍*6を定める。このとき、ここで定められた加法とスカラー倍が次の条件を(１)ー(８)を満たすとき、VをK上の線形空間という：a,b,c∈*7Vとしα,β∈Kとする。

(1)  a + b = b + a

(2)  a +(b + c) = (a + b) + c

(3)  Vには零元0*8が存在し、すべてのa∈Vに対して、a + 0 = a を満たす。

(4)  各a∈Vには逆元と呼ばれるb∈Vが存在し、a + b = 0 を満たす。

(5)  1a = a

(6)  α(a + b) = αa + αb

(7)  (a + b)α = αa + αb

(8)  α(βa) = αβa

（以下数学定義の引用は磯祐介『ライブラリ理工新数学‐T4：新しい線形代数学通論』2014、サイエンス社）

　ちなみに、途中で途切れた直線や平面の一部分は線形空間にはなりません（要素の和が常にその集合の要素にならないといけないので）。この線形空間というものを議論するときにお役立ちなのが、線形独立、基底、次元という概念です。

　ここからが新しい話です。

線形独立

　線形空間という集合の中の、いくつかの要素を取ってきたグループについて言う性質です。浅野さんの連作空間論にはでてきませんが、これは基底や次元の話のまえにおさえなきゃな概念なので書きます。前の記事で、線形独立というのは、ざっくりそれぞれ違った向きのベクトルの集まりを指して言う、と書きました。線形空間の中のベクトルは、それを足したりやスカラー倍したりそれをまた足したりしても、ちゃんとベクトルであり、その線形空間にふくまれます。逆に考えて、線形空間の要素を一つとって、他の適当なベクトルの式で表すことができます。その線形空間の中で、線形独立なベクトルの集まりがあったとき、そのベクトルたちはみんな違う向きを向いているので、線形独立なベクトルたちのどの要素も、残りの線形独立なベクトルで表すことができません。という話を数学的に書いたら下の話になります。

　数式を入力するということに対して技術的に敗北したのでワードの画像です。フォントだとわかりにくいんですが、ベクトル（線形空間の要素）には普通のアルファベットのaを（といっても数式で入力したのでちょっとフォントが違って見えますが）、スカラー（つまり数字）（Kの要素）はアルファで表されていて、この違いは大事なので注意してください。下の添え字はとりあえずとってきた順番に番号を振りました～って感じのやつです。そして、｛｝はその中身が集合であることを示す記号です*9。そこにk＝1, nという記号があります。これはkが1からn(場合によって決められる適当な自然数)までひとつずつという意味で、結局は{a_1, a_2, a_3,…a_n}と書くところをらくしているわけです。

　この{a_1, a_2, a_3,…a_n}*10の線形結合、というのは、とりあえずとってきたベクトルたちの集合から足し算したりスカラー倍したりスカラー倍したものを足し算したりしてできるベクトルを、とても一般的な形にして表したものです。こうやって、このベクトルたちの線形結合、という風に書くことで、ベクトルたちの集まりの要素を足し算したりスカラ―倍したり…と長々言わないで済ませられます。

　｛｝が集合の記号であったように、〈〉が線形包の記号です。この前わたしがspan（）と書いたのも同じく線形包の記号です。

　{a_1, a_2, a_3,…a_n}の線形結合の全体というのは、a_1や a_2や …a_nたちといろんな数を使って表すことができるすべてのベクトルということです。{a_1, a_2, a_3,…a_n}は要素の数がn個の集合ですが、〈a_1, a_2, a_3,…a_n〉になるともとの要素を好き勝手伸ばしたり足したりしたもの全部を含めるので、とても広がります。　

　( x , y )という形式で表される２次元ベクトルの集合として、x軸とy軸をもつ平面座標を考えてみてください（図を出すべきなんですけどさぼります、必要に応じて紙にxy座標軸を書いてもらえたら…）。この平面座標も線形空間です。ℝ×ℝやℝの2乗と書いて表します*11。その中の２つの要素をとってきた{ ( 0, 1 ) , ( 1, 0 ) }は元が２つの集合です。この集合の線形包〈 ( 0, 1 ) , ( 1, 0 ) 〉はもとの平面全体になります。平面上のすべてのベクトルを、( 0, 1 )と( 1, 0 )の線形結合（足し算したりスカラー倍したりそれを足したり）で表すことができるからです。〈 ( 0, 1 ) , ( 0, 8 ) 〉の場合も考えてみましょう。( 0, 1 )と( 0, 8 )の線形結合で表すことができるのは、y軸上の数だけです。線形結合によって好きな数字をy座標にすることはできますが、x座標はゼロのままです。つまり、〈 ( 0, 1 ) , ( 0, 8 ) 〉はy軸である、と言うことができます。

 　磯先生の本は一次独立と書いていますが、いろんな用語があるだけです。用語の歴史や使い分けはあまり調べていないのであれですが。Σ（シグマ記号）はそのあとに来たものを添え字の数が動く間は足し算しろ、という記号です。シグマ記号にびびる人は、紙と鉛筆を持ってきて、線形結合の引用のところみたいに足し算に開いて式を書いたらいいと思います。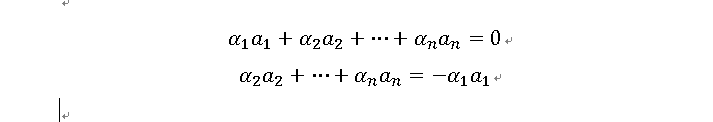

　このように式変形すると、下の式では、ベクトルa_1（のスカラー倍）がほかのベクトルの線形結合で表されています。ここで、この式はベクトルの係数アルファkがすべて零の時しか成立しない、と線形独立の定義を見ると、どのベクトルもほかのベクトルの線形結合で表すことができない、ということが必要十分条件であると分かります。

　さっきのxy座標空間の例でいえば、( 0, 1 )と( 0, 8 )はそれぞれのスカラー倍で相手を表すことができるので線形独立ではありません（これを線形従属／一次従属と言います）。そして( 0, 1 )と( 1, 0 )の場合はお互いがお互いをスカラー倍で表すことができないので線形独立ですね。なんだか同じ数のベクトルがあっても、線形独立なベクトルの組のほうが豊かな感じです。

基底

 　さっき線形包の話をしたところで、線形空間である2次元ベクトル空間がその二つの要素 ( 0, 1 )と( 1, 0 )の線形包 〈 ( 0, 1 ) , ( 1, 0 ) 〉によって表せてしまいましたね。このように、線形空間V（と名付けましょう、いま名付けました）の元｛a_1, a_2, …a_n｝（いくつかベクトルをとってきてaとその添え字で管理しましょう、今決めました）の線形結合でVのすべての元を表すことができる、ということがあります。記号で表せば、

V＝〈a_1, a_2, …, a_n〉

 です。便利ですね、記号大好きです（電子的に入力しようと思わない限りは）。線形空間Vとベクトルの組｛a_1, a_2, …a_n｝がこういう関係になっているとき、｛a_1, a_2, …a_n｝をVの生成系と呼びます。単なる呼び方の話です。

　有限生成というのは、V＝〈ベクトル、ベクトル…〉ってなっているとき、その〈〉のなかのベクトルの数が有限個だということです。

　その線形空間を無駄なく張る*12ことができるベクトルの組を、その線形空間の基底である、って感じです。

　2次元数ベクトル空間において、{ ( 1, 0 ), ( 0, 1 ) }は基底です。{ ( 2, 1 ), ( 1, 0 ) }や{ ( 1/2, 1 ), ( -1, 15 ) }だって基底になれます。これらは線形独立なベクトルの組であり、その線形包がちゃんともとの2次元数ベクトル空間になるからです。{ ( 0, 1 ), ( 0, 8 ), ( 1, 0 ) }はどうでしょう。これらの線形包も、確かに2次元数ベクトル空間を構成します。

〈( 1, 0 ), ( 0, 1 )〉＝〈( 2, 1 ), ( 1, 0 )〉＝〈( 1/2, 1 ), ( -1, 15 )〉であり、

〈( 1, 0 ), ( 0, 1 )〉＝……＝〈( 0, 1 ), ( 0, 8 ), ( 1, 0 )〉です。

　しかし、{ ( 0, 1 ), ( 0, 8 ), ( 1, 0 ) }は線形独立なベクトルの組ではありません。そのため{ ( 0, 1 ), ( 0, 8 ), ( 1, 0 ) }は基底ではありません。ちなみに、数ベクトル空間で(1, 0, 0,…), (0, 1, 0, 0,…), (0, 0, 1, 0, …), … (0,…,0, 1)と表されるきれいな基底を標準基底とよび、e（と次元の数だけの添え字）で表します。{ ( 1, 0 ), ( 0, 1 ) }は2次元数ベクトル空間の標準基底で、｛e_1, e_2｝と書かれます。

　また前回の記事の例を思い出してみましょう。

　

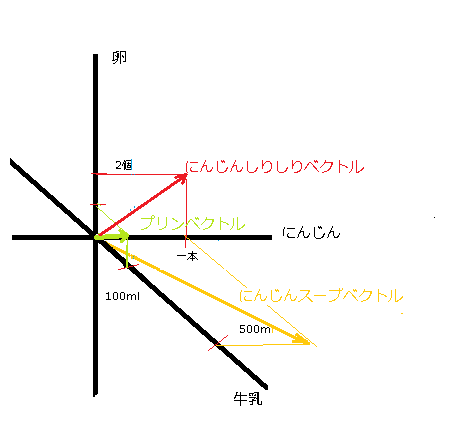
　ここでは、｛卵ベクトル、にんじんベクトル、牛乳ベクトル｝や｛プリンベクトル、にんじんしりしりベクトル、にんじんスープベクトル｝、｛にんじんしりベクトル、にんじんベクトル、にんじんスープベクトル｝は基底ですが、｛卵ベクトル、にんじんベクトル、牛乳ベクトル、プリンベクトル｝や｛にんじんベクトル、にんじんスープベクトル、牛乳ベクトル｝は基底になりません。｛卵ベクトル、にんじんベクトル、牛乳ベクトル、プリンベクトル｝において、プリンベクトルは卵ベクトルと牛乳ベクトルの線形結合で表せてしまうので、このベクトルの組全体は線形独立ではありません。また、｛にんじんベクトル、にんじんスープベクトル、牛乳ベクトル｝でもそうです。

　少し例が冗長になってしまいました。たくさん例を挙げて、基底について確認したかったことは次の二点です。

・基底は何通りも取り方がある

・同じ線形空間の基底は選び方が異なっていても数がおなじ

これはちゃんと定理として証明されていることがらです。

次元

（次元）　Vを体K上の有限生成の線形空間とする。このとき、Vの基底の元の個数をVの次元（dimension）といい、記号ではdimVと表す。Vが有限生成でない*13ときはVを無限次元線形空間であるといい、dimV=∞とする。

　基底まで来たら次元は簡単ですね。基底は何個ですか？というのが次元です。

　このあたりの基底や次元の性質によって、同じ次元の線形空間は大体似たようなものとして同一視して扱えます。例えば実数（複素数でもよい）係数n次の多項式の全体も、加法とスカラー倍を定義することができて線形空間になるんですけど、それについて議論するときは、n次元だから似たようなものだよね～っていってn次元数ベクトル空間みたいにして考えることができます。

軸

　軸ってなんなんでしょうね。今まで軸の定義ということをしたことなしに、ふんわり使っていました。磯先生の本でも定義なしで出てくるし、たぶんほかの線形代数の本でも分かってるよね～って感じでしか出てこないんでないでしょうか。典型的には、数ベクトル空間の標準基底の延長したものと一致するものを座標ってよぶことが多いと思うのですが、それだけではないですしね……

　困ったときは参考図書、ということで図書館で二、三冊ぱらぱらしてみました。いくつか関係ありそうな記述があったので引用します。

【座標】coordinates

　ユークリッド平面（空間）の点に数の組を対応させること。デカルト、フェルマによって考えられたが、その源流はアポロニオスの円錐曲線論にある。

【座標軸】coordinate axis

　 平面あるいは空間上に*座標（正確には直交座標を）を定めるには、原点、単位の長さと互いに直交する２個（空間の場合は３個）の方向を定める必要がある。 すなわち、x軸、y軸（およびz軸）の方向を定める必要がある。この２つないし３つの原点を通る直線（すなわちx軸、y軸（およびz軸））のことを座標軸 と呼ぶ。４次元以上でも同様である。

　座標軸が必ずしも直交しない場合も座標が定まり、これを*斜交座標という。

【ユークリッド空間】Euclidean space

　平面、３次元空間などの概念の高次元版である。n個の実数の組全体Rのｎ乗に、（引用者注：…式の入力に力尽きたので内積の定義式省略、常識的に知られている内積です…）なる内積を入れて考えたものである。ユークリッド距離*14を考えて、距離空間とみなす。

　ユークリッド空間というときは、特定の座標の取り方や原点の取り方は、決めずに考える。…

（『岩波　数学入門辞典』、2005、岩波書店）

 　忘れてましたけど座標軸は原点を通るっていうの大事ですね。

【ユークリッド空間】…

　ユークリッド幾何学の公理をみたす空間を、ユークリッド空間という。実数体Rの上のn次元ユークリッド計量線形空間を基準ベクトル空間とするアフィン空間がn次元ユークリッド空間（n-dimensional Euclidean space）Eのｎ乗*15である。（…中略）この意味でEのｎ乗とRのｎ乗＝｛(x_1, x_2,…, x_n) | x_i ∈R ｝とは一対一に対応づけられる。この意味でEのｎ乗とRのｎ乗とを同一視してRのｎ乗自身を単にユークリッド空間と呼ぶことが多い。（中略…）ユークリッド空間Rのｎ乗の点xはｎ個の実数の組(x_1, x_2,…, x_n) によってあらわされ、（中略…）、x_i を点ｘの第i座標（i-th coordinate）,点（0, 0,…,0）を Rのｎ乗の原点（origin）、点集合｛ｘ｜-∞ < x_i < ∞ , x_j = 0 (j ≠ i)｝*16をx_i軸（axis）または第i座標軸(coordinate axis)という。

（『岩波　数学辞典第四版』2007、岩波書店）

【初等幾何】

…座標導入のアイデアはそもそもは１６世紀のデカルト（Descartes）によるが、平面上の点や図形の位置が座標によって記せることの恩恵は大きい。たとえばR×R（引用者注：Rの２乗と表記されている）は、成分ごとの加法に関してR上のベクトル空間とみなすことができる。…

…平面Rの２乗に、長さや角度を測る基礎となる内積（１）（引用者注：その前のほうで定義されている）を付随させて、とくにユークリッド平面（Euclidean plane）と呼びEの２乗で表す。すなわちユークリッド平面とは、平面Rの２乗に直行座標系という情報を付け加えた幾何学の台空間のことで、直線に座標を入れた実直線に対応する。

（『朝倉　数学辞典』、2016、朝倉書店）

　　もっと調べたら前記事から適当に扱っているユークリッド空間と数ベクトル空間と平面R×Rのことが解決するかもですね。でも私に時間がないのでおいときます。というか辞典ごとで微妙に定義の仕方や出発点が違う感じがして難しい。

　あまりしっかり分かった気がしませんが、とりあえず座標軸とは、

・平面や空間（ｎ次元も）に（？）導入される、点を数の組で表すシステム座標の道具

・座標によって定められた原点を通り、第なんとか座標の値を定める直線

・線形空間の次元と同じ数ある

ってぐらいのイメージで行こうと思います。

　基底と座標軸ってどういう関係なんでしょう、最初の引用の中の定義では、軸だって自由に定めることができそう（実際斜交座標みたいなものはある）ですが、二番目の引用の中のRのｎ乗の場合は軸は一意的に定めることしかできません。基底はベクトル（線形空間の元）であり、基底の一つ一つを任意にスカラー倍した集合は、それぞれ原点を通る直線になって、軸っぽさもあるようなきがするのですが……わからない。

基底空間

　辞書の索引で調べたんですが一個もでてきませんでした。語から類推しようにも、基底（によって張られる）空間、だった場合、それはそれを基底とする線形空間自体になるのでちがうよなあ。数学用語に探すのはあきらめます。

　とにかく、ここでようやく「連作空間論」にこっそり登場する道具をそろえることができました。この数学的道具と「連作空間論」を比べてみて思ったことや、無限次元線形空間へのロマンの話をするのが全体の話の適切な着地点なんだろうと思うのですが、卒論の首が回らなくなってきて書けるかどうか非常にあやしいので、めちゃざっくりメモだけして終わりにします。

• 連作から読むことができる作品世界、というのと、連作（をベクトル的にとらえて）その歌たちの線形包として構成される〈連作空間〉*17（という線形空間的な存在）という対応づけや、「〈連作空間〉には〈私〉が触れうる範囲のありとあらゆるものが存在している。であれば、〈連作空間〉と連作はイコールではないだろう。」というのは、上のような線形代数の話を知っていると大変共感した。

• 「〈基底〉とはつまり、〈連作空間〉の内部の事物を、その性質や概念などに応じてつなぎ合わせるベクトルである。」「〈基底〉によって〈連作空間〉の中のあるまとまった範囲の情報を表現することが可能である。この〈連作空間〉に〈基底〉によって設定された限定的な空間が〈基底空間〉である。」は分からない。
• 線形代数の話を忘れて考えると、歌と歌とのつながりによって見える道筋とが〈基底〉で、その文脈的な拡大が〈基底空間〉という風に読むことができるだろうか。でも、線形代数の話を思い出すと、そもそも基底によって表現される範囲って基底の定義からして線形空間全部になるやん、わからん、みたいになる。そのためその後の基底や基底空間の説明をうまく呑み込めていない…

• 「ある連作の作品世界を把握するために必要になる評価のための軸を〈連作軸〉と呼び、その個数を〈次元〉と呼ぶ」と〈次元〉を定義されると、数学の次元が基底により定義されることから、逆算されて〈連作軸〉って基底（線形空間でいう）やん、といいたくなってしまう（言いがかりかもしれない）。
• 連作の作品世界と線形空間を対応させることの良い点として、私は基底の付け替えができること、つまり、同じ現象に対して違った仕方で評価ができる点というのを見たい。しかし浅野さんが連作軸を基底的な付け替え可能なものとして見ているのかどうか、このあたりの概念のところがいまいち釈然としない。

• 最初に連作軸を評価のための軸だと定義したあと、「読者という〈連作軸〉」が後ろのほうで登場してくるのは混乱した。でもこのあたりが、人によって連作の評価軸（これは自然言語の意味での軸）が違うということを汲んでるのかな。

• これに関連して、前衛短歌において「実世界の作者としての〈私〉と、作品世界としての〈私〉。この複合的な〈私〉の様相により、連作中の世界はより広がりを見せることとなった。」と述べられているけど、前衛短歌の読みの中で、（短歌が私性から逃れられないのはそうだけど、）作者の〈私〉を離れて薄く存在する作品世界の〈私〉に注目する、というのはそんなに批評の要点なのかよく分からなかった。

• 無限次元線形空間の話はたいへんわくわくするので将来的に勉強できたらいいなあ。ベクトルと関数は同じ視点から考えることができる、と初めて聞いたときはめっちゃテンションあがった。ベクトルー無限次元ベクトルー関数（多項式関数だけでなく、三角関数や指数関数も）が、有限ー加算無限ー非加算無限という整理で統一的に表せる、ということに関連してこのHPの図は、ベクトルと関数を同じように扱えるんだ！ってきれいに見えるからたのしい。

  線形代数II/関数空間 - 武内＠筑波大

*1:このタイプの議論の例としては、∧（かつ）や⇒（ならば）などの論理記号が実際に数学における関数の概念として理解できる！といった論理革命があるのかなあ、と思います。最近講義でちらっと聞いておもしろい！！と思っただけなので論理革命については出典が分かりません。

関数とは、ある集合の要素（一つでも複数でもいい）を、別の集合の要素一つに対応させる写像として捉えられます。ものを入れたらものが出てくるというやつです。そして論理記号は、個々の命題の真理値を連結した命題の真理値へ移す、真理値から真理値への写像というわけです。

*2:前記事末尾のメモで触れたように、短歌に交換可能な加法乗法は成立しない

*3:体：普通の（順番を変えたり複数回おこなっても答えが変わらない）足し算と掛け算ができて、その答えも自らのうちに含む数の集合のこと。当座の理解では私たちが知ってる数だと思って大丈夫です。つまり掛け算足し算はあたりまえでなくて、それが普通じゃないものについても想定しているわけですよね。数学のこういうところさいこーじゃないですか？そうやっていろんなことが自明じゃないかもしれないってやるから定義の文章とかがややこしくなるんですが……

*4:ℝ：実数real numberの記号。ちなみにこのℝという書かれ方は、手書きの時などに太字ということを表すための書き方です。Rと書く本もあると思います。

*5:ℂ：複素数complex numberの記号

*6:スカラーっていうのは数のことです、たぶん。ベクトルという数ではないものに対して、数字をかけたもの、ということでスカラー倍と言われています。

*7:∈：含まれる、という記号。ここではa,b,cがVという集合の要素であることを示す

*8:数学の記号に太字が出てきたら、ベクトルを表している。これは数字のゼロではなくて、ゼロベクトルの意味

*9:たとえば自然数という集合を｛1, 2, 3, …｝と表すことができる

*10:これはa_1, a_2と名前をとりあえず付けてみたベクトルたちの集合

*11:実数の軸が2つあるということですね。ℝの2乗と書くほうが一般的な表記な気がしますが入力能力がなくてその…

*12:ベクトルとかの話をするときに、かなりナチュラルに「張る」という言葉を使ってしまうのですが、線形結合で表す、ぐらいのつもりで言っています。

*13:有限個の元をどのように選んで線形包をとっても、Vにならない場合

*14:常識的に知られている距離と思ってもらえば

*15:表記あきらめました、すみません

*16:{　}のなかに縦棒｜が入っている記号は、この要素のうちこんな性質をもってるやつの集合といういみです。このばあい、ｎ個の実数の組で表せる点ｘ（という名前を便宜的につけた）のうち、、あるi番目の要素以外は全部ゼロで、i番目の要素は何をとってもいい点（無限にある）の集合ということをあらわしています。

*17:混乱してくるけどこの〈〉カッコは線形包のかっこではない